Swapping Knights
You have a chess configuration as:
How can you move the knights in any order so that it can look like:
That is:
Visualization & Solution
Imagine that you have a knight on A1, and you need to map out the possible movements for this knight. At the start it can only move to either B3 or C2. Let’s just take the path B3. Then we take C1, A2, C3, B1, A3, C2, A1. As you can see, our knight took an entire tour around this board and returned to the original position. This must mean that if we start the knight on any tile that is not B2, you can always reach some other point. Furthermore, if you are perceptive enough, you can tell that for a path of a single knight, we visited every position except for B2 once.
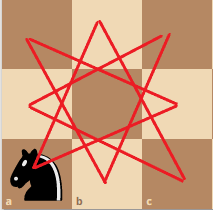
Then, imagine our board as a graph, with each position on the board as a vertex.
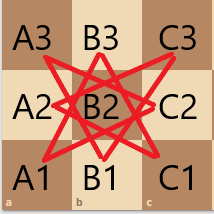
Using the last piece of information we gained, if the look at the board with a perspective of a graph, we can ascertain that the graph is representative of a cycle, and the path of the knight is an eulerian cycle.
Let’s take the first configuration and add the other knights in their respective positions on the board and expand the board into a graph. We have:
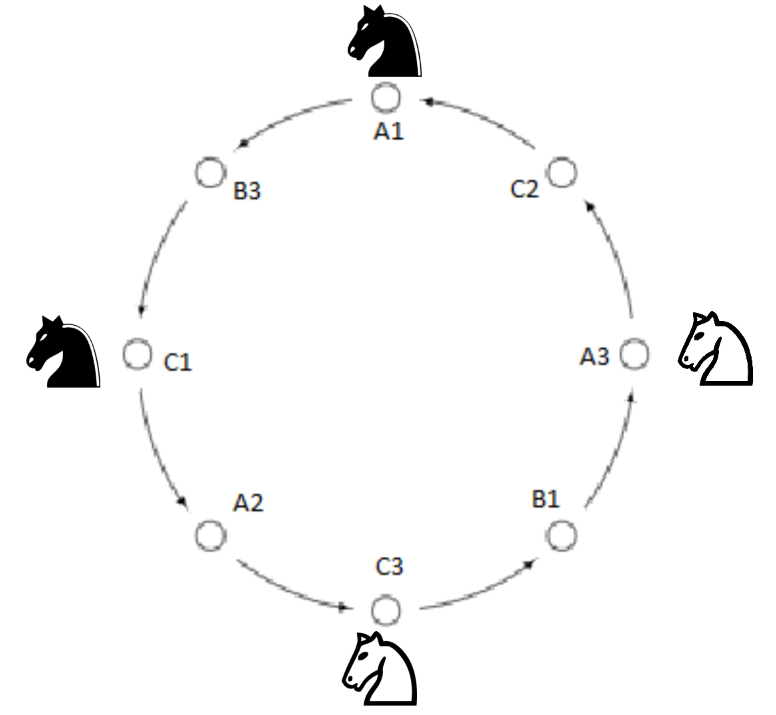
From this graph, the white knight at A3 can go from A3 to C2 as well as A3 to B1. However, the white knight cannot move from C2 to A1 since the black knight is blocking the path.
Now here is the second configuration we want to achieve with the knights in their respective positions on the board:
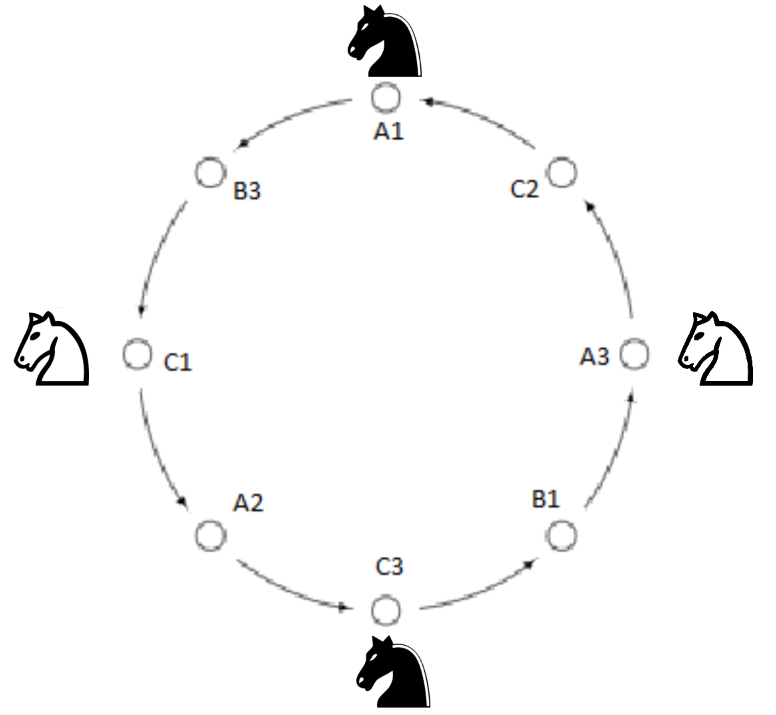
As you can see, this configuration requires the neighboring knights to be of different color. However, achieving this configuration from the first configuration is impossible since one of the knights will have to swap places with another knight.
Solution
Therefore, we cannot move the knights in any way to achieve our configuration.
This work is licensed under CC BY-NC-SA 4.0
