Peaceful Rooks

You have a chess board, which is a 8 x 8 board, and you want to have 8 peaceful rooks live in harmony together. Then, because you are a mathematician (and a masochist), you want to find out how many different positions we can place these rooks so that they are all peaceful.

A peaceful board state is where none of the pieces can attack another piece (you can even say that starting out a chess game the board is peaceful). Here is an example of a peaceful board.

As you can see, none of the rooks are attacking each other.

It is your job to find all of the possible peaceful states for these rooks.

Problem Statement

For a board with size n x n, and n rooks. How many ways can n rooks be places s.t. they are peaceful?

Visualization

Let us assume that we have some function Q, which defines as Q(n) = number of configurations of n peaceful rooks in a (n x n) board.

If we have a 1x1 board, then it is obvious that Q(1) = 1.

What if we have a 2x2 board? Easy. Here are the possible configurations, resulting in Q(2) = 2.

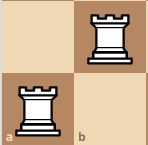
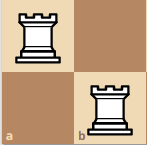
3x3 board. Q(3) = 4

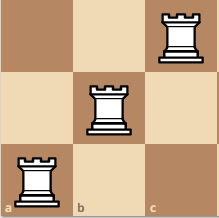
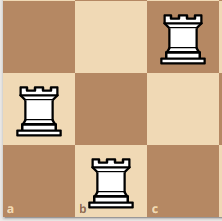
4x4 board. Q(4) = 10

Examine

We don’t have a pattern yet, but we can assume that there is likely a pattern going on here. For instance, you might recognize similar rook layouts from the 2x2 board that appears on the 3x3 board or 4x4 board. This is no coincidence, there IS a pattern! We just need to decipher the problem further.

The best way to start out is to look at the baseline, the 1x1 board. We know that Q(1) is the smallest board state we can have. Thus, we can say that Q(1) is our baseline. Then in a 2x2 board, there exists 4 total possible combinations of rooks in each position. However, only two of them have peaceful rooks, so we can include Q(2) = 2 as another base case. The reason why I am including these two as base cases, would matter a bit more afterwards, but since we already know the answer for Q(1) and Q(2), might as well set those to true.

In a 3x3 board, there is a total of 9 different positions with various combinations of peaceful rooks. For instance, one possible placement is when all of the rooks are diagonal to each other. Here is an example

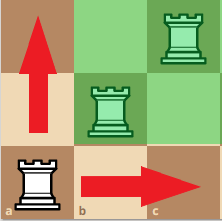
Let us visualize the bottom left rook. The red arrows display all the possible positions where this rook can attack. Thus, any other position that we place the other two rooks can only be inside of the green square. If you look at the green square, we can see that this configuration is similar to our 2x2 board congiruation! Even if we use the other pattern it is valid.

Let’s call this rook the “pivot rook”.

What if we move the bottom left root up one space? Then, the rook in the middle must move away from the center to the bottom s.t. the rooks can be peaceful.

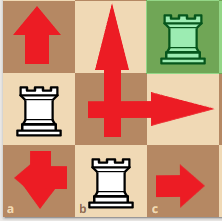
So if the middle rook has to move down one space for this configuration, the only configurations allowed for the top right rook has to be inside of the green square (which is one).

Finally, if we move the rook up one more step, then we have to move the rook in the bottom middle up to the middle and the room to the top right all the way down.

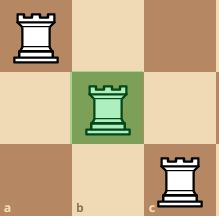
All in all, just based of from one rook moving, we can find all of the configurations for this 3x3 board. Why is that so? If we take any other rook and move it likewise, it will create the same pattern we did with the bottom right rook we moved. Furthermore, if we look at the total amount of configurations, especially by examining the green squares, we can add up the amount of total peaceful rooks as:

Q(3) = Q(2) + Q(1) + Q(1) = 4

We know that Q(3) = 4, and this is correct! Is this another coincidence? Well… let’s find out.

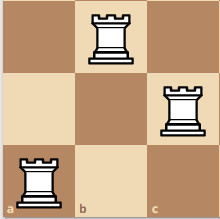
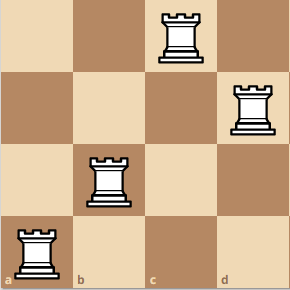
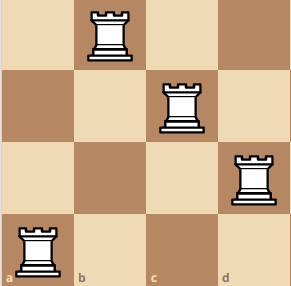
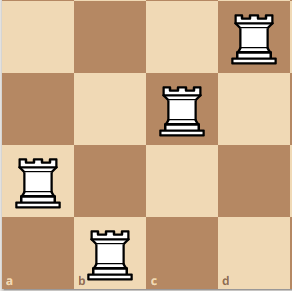
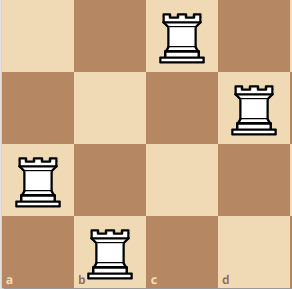
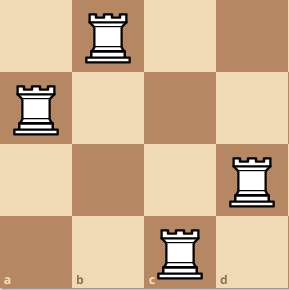
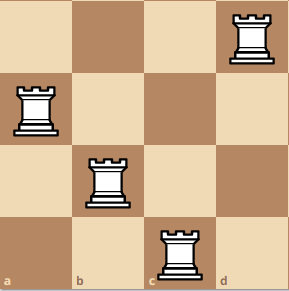
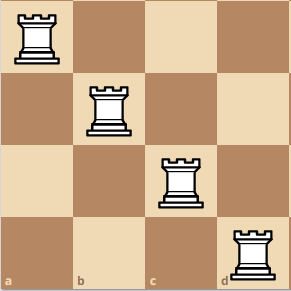
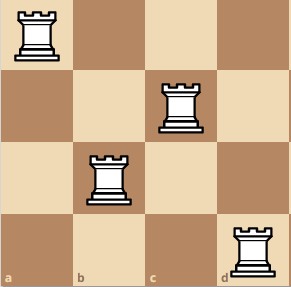
Here is a larger example with more visualization. A 4x4 board.

Lets start at some diagonal position, and take the bottom left rook as the pivot rook. At this position, ignoring the red squares, we can make a smaller 3x3 board which yields four different arragements.

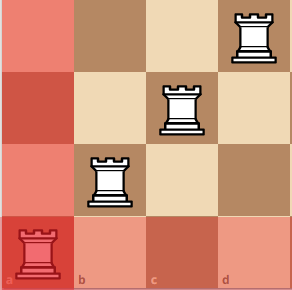
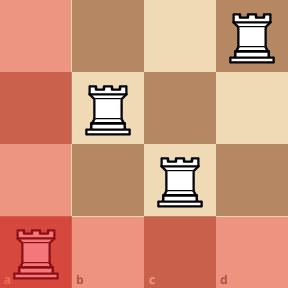
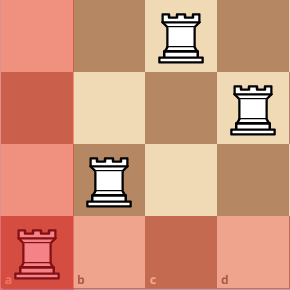
Then, we can move the pivot rook up, here you can see that we created a 2x2 board.

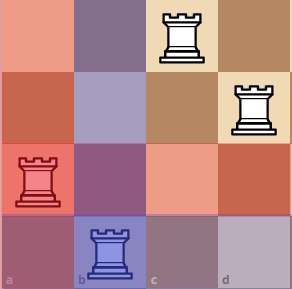
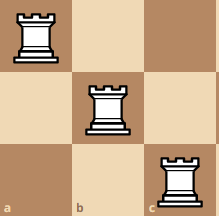
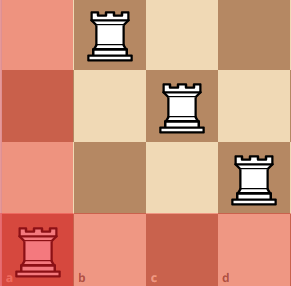
If we move the pivot rook up again, we get a weird configuration like this:

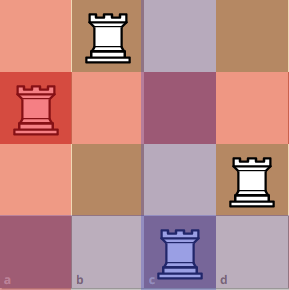
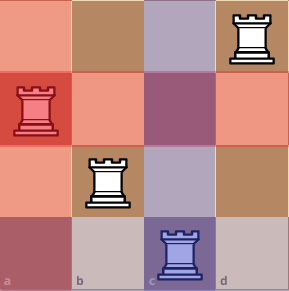
Although it does not seem like we can use the configuration from another board, there is a hidden board here! If you take all of the squares and then removed all of the squares with the color blue and red, you will get a board with an island of different squares. We can combine these board, and create a pseudo-board. This is practically a replication of a n x n board due to however many squares are left. Moreover, since we are not using the squares that are being attacked by the other rooks, we can guarantee that these squares are different combinations.

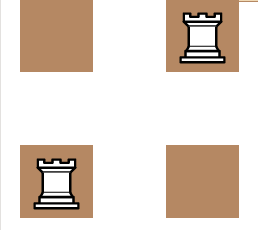
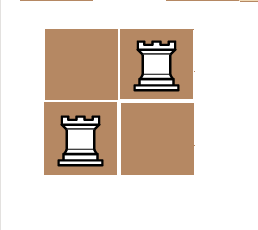
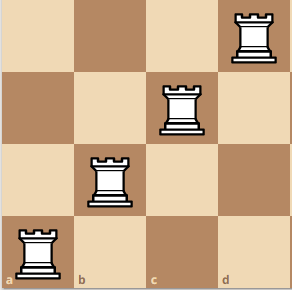
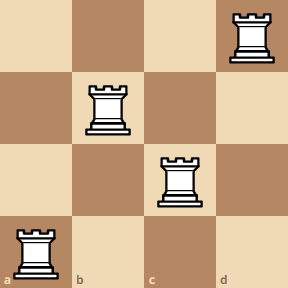
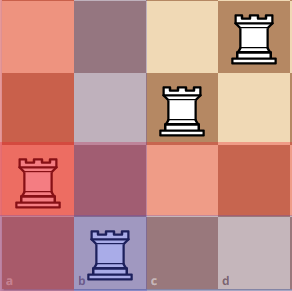
Finally, we move the pivot rook up again, which will create the configuration here.

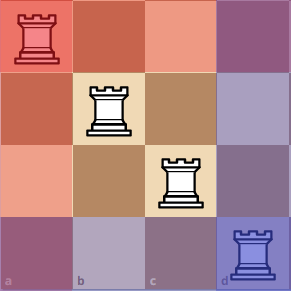
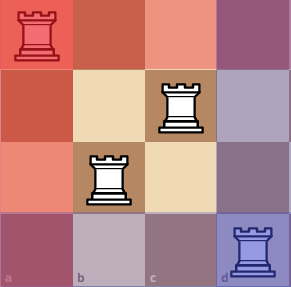
Combining all of the results, we get Q(4) = 4 + 2 + 2 + 2 = 10. Do you see the pattern now? Since we move the pivot rook 4 times, we add 4 times, based on the total amount of confiurations that we can have. Then, we can say Q(4) is equivalent to Q(4) = Q(3) + Q(2) + Q(2) + Q(2).

That means if we start with a diagonal, and using the property of the pivot rook moving upwards, we can guarantee that the first pattern uses the peacful board combinations from Q(n - 1). Then for each other term that we add up, it will be Q(n - 2) since we have to move another rook when we move the pivot rook.

Finally, we can come up with this:

Q(n) = Q(n - 1) + Q(n - 2) * (n - 1)

Solution

Let Q(n) = number of configurations of n peaceful rooks in a n x n board.

Q(n) = Q(n - 1) + Q(n - 2) * (n - 1), where Q(1) = 1 and Q(2) = 2.

Such an elegant solution.

Code

Note that we do

Q[i] = Q[i - 1] + Q[i - 2] * (i)

since i is 0th indexed.

def solution(n):
    if n == 1 or n == 2:
        return n
        
    Q = n * [0]
    Q[0] = 1
    Q[1] = 2
    
    for i in range(2, n):
        Q[i] = Q[i - 1] + Q[i - 2] * (i)
    
    return Q[n - 1]

print(solution(3)) ———- 4
print(solution(4)) ———- 10
print(solution(8)) ———- 764
print(solution(50)) ———- 27886995605342342839104615869259776

If you’d like to check my work or want me to write a proper proof, please do a 50 x 50 chess board on paper.

End

Thank you for reading and have a good day.

This work is licensed under CC BY-NC-SA 4.0