L2-regularized Logistic Regression

Logistic regression is a very popular algorithm as it is fast to use and generally reliable for regression problems. L2 regularization or ridge regression or more commonly known as weight decay, is a technique that modifies a loss function by adding a regularization term to penalize drastic changes in the weight fitting well with the data. Here, I provide the derivation for l2-regularized logistic regression

In order to derive the loss for logistic regression, we need to compute the gradient and hessians of that loss function. First we can define the function as:

$$ f(ω’) = \frac{1}{n} \sum_{i=1}^nlog(1 + exp(-y_i(ω_0 + ω^Tx_i))) + λ ||ω||_2^2 $$

Furthermore, note that the bias is not regularized; therefore, we consider $ω_0 = [ω_0; ω]$ as the vertical concatenation of the bias and feature coefficients. Before we find the gradient, it is imperative for us to break down the function to help. Moreover, let us define another separate function that will come into use later.

The Sigmoid Function ($\sigma$)

The sigmoid function, which is generally represented as $\sigma$, is $$\text{sigmoid}(x) = \frac{e^x}{1 + e^x} = \frac{exp(x)}{1 + exp(x)} = \sigma(x)$$

visualized sigmoid function

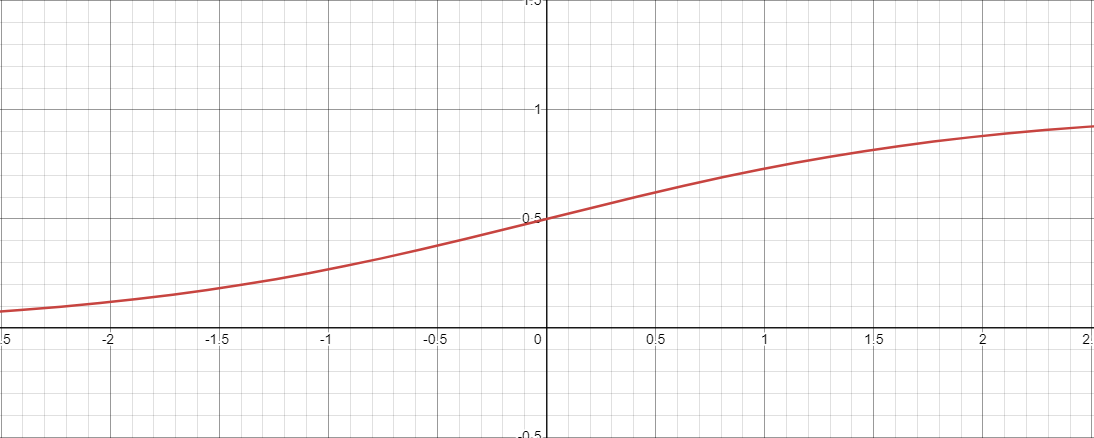
Prior to it’s now common use for machine learning as an “activation function”, in a general sense, it is just a function that maps a value (x) to another value between 0 and 1. In a binary problem, we see this as an arbitrary number that evaluates to either true or false according to the input value.

Moreover, let us find the derivative of the sigmoid function (hint: we will need it later)

I’m too lazy to add the derivation for this. here it is.
$$ \sigma’(x) = \sigma(x)(1-\sigma(x)) $$

blue line is the derivative of the sigmoid function

Computing for $∇_{w’}f$

In order to find the gradient, we need to find the derivative of the function according to the bias and feature coefficients. The order does not matter much.

$$ ∇_{w’}f = [\frac{\partial f}{\partial w_0}; \frac{\partial f}{\partial w}] $$

Finding $\frac{\partial f}{\partial w_0}$

Here we apply $\frac{\partial}{\partial w_0}$ and separate for simplicity

$$ (\frac{\partial}{\partial w_0})(\frac{1}{n} \sum_{i=1}^n \log(1 + \exp(-y_i(ω_0 + w^Tx_i))) + λ ||w||_2^2) $$

we can ignore the summation since it applies to all n, it wont change the derivative (we will have to substitute it back later)

$$ (\frac{\partial}{\partial w_0})\log(1 + \exp(-y_i(ω_0 + w^Tx_i))) + ((\frac{\partial}{\partial w_0})λ||w||_2^2) $$

we can separate the into two parts to make it easier to derive overall

• Derive $(\frac{\partial}{\partial w_0})λ||w||_2^2$:

  $$ (\frac{\partial}{\partial w_0})λ||w||_2^2 = 0 $$

• Derive $(\frac{\partial}{\partial w_0})\log(1 + \exp(-y_i(ω_0 + w^Tx_i)))$:

  $$ (\frac{\partial}{\partial w_0})\log(1 + \exp(-y_i(ω_0 + w^Tx_i))) $$
  apply the derivative due to log
  $$ \frac{1}{1 + \exp(-y_i(ω_0 + w^Tx_i))} * \frac{\partial}{\partial w_0} (1 + \exp(-y_i(ω_0 + w^Tx_i))) $$
  apply the derivative again due to the exponent
  $$\frac{1}{1 + \exp(-y_i(ω_0 + w^Tx_i))} * (\exp(-y_i(ω_0 + w^Tx_i)) * (\frac{\partial}{\partial w_0} * -y_iω_0 - y_iw^Tx_i)) $$
  apply the derivative, we can remove the term on the right since it is $w^T$
  $$\frac{1}{1 + \exp(-y_i(ω_0 + w^Tx_i))} * \exp(-y_i(ω_0 + w^Tx_i)) * -y_i $$
  combine the terms together
  $$-y_i * \frac{\exp(-y_i(ω_0 + w^Tx_i))}{1 + \exp(-y_i(ω_0 + w^Tx_i))} $$
  using the sigmoid function we defined earlier, we can dress up the function
  $$ -y_i * \frac{\exp(-y_i(ω_0 + w^Tx_i))}{1 + \exp(-y_i(ω_0 + w^Tx_i))} \rightarrow -y_i *\sigma(-y_i(w_0 + w^Tx_i))$$

Then place all derived values back into $\frac{\partial f}{\partial w_0}$,

$$ \frac{1}{n} \sum_{i=1}^n ((\frac{\partial}{\partial w_0})\log(1 + \exp(-y_i(ω_0 + w^Tx_i)))) + ((\frac{\partial}{\partial w_0})λ||w||_2^2) $$

$$ \frac{1}{n} \sum_{i=1}^n -y_i *\sigma(-y_i(w_0 + w^Tx_i)) $$

$$ \frac{\partial f}{\partial w_0} = - \frac{1}{n} \sum_{i=1}^n y_i *\sigma(-y_i(w_0 + w^Tx_i)) $$

Finding $\frac{\partial f}{\partial w}$:

follows the same format as before

$$(\frac{\partial}{\partial w})(\frac{1}{n} \sum_{i=1}^n \log(1 + \exp(-y_i(ω_0 + w^Tx_i))) + λ ||w||_2^2)$$

$$\frac{1}{n} \sum_{i=1}^n ((\frac{\partial}{\partial w})\log(1 + \exp(-y_i(ω_0 + w^Tx_i))) + ((\frac{\partial}{\partial w})λ||w||_2^2) $$

• Derive $(\frac{\partial}{\partial w})λ||w||_2^2$:

  $$ (\frac{\partial}{\partial w_0})λ||w||_2^2 = 2\lambda w $$

• Derive $(\frac{\partial}{\partial w})\log(1 + \exp(-y_i(ω_0 + w^Tx_i)))$:

  $$ (\frac{\partial}{\partial w})\log(1 + \exp(-y_i(ω_0 + w^Tx_i))) $$
  apply the derivative due to log
  $$ \frac{1}{1 + \exp(-y_i(ω_0 + w^Tx_i))} * \frac{\partial}{\partial w} (1 + \exp(-y_i(ω_0 + w^Tx_i))) $$
  apply the derivative again due to the exponent
  $$ \frac{1}{1 + \exp(-y_i(ω_0 + w^Tx_i))} * \exp(-y_i(ω_0 + w^Tx_i)) * (\frac{\partial}{\partial w} * -y_iω_0 - y_iw^Tx_i)) $$
  apply the derivative, and we dont eliminate the right term this time
  $$ \frac{1}{1 + \exp(-y_i(ω_0 + w^Tx_i))} * \exp(-y_i(ω_0 + w^Tx_i)) * -y_ix_i $$
  organize the function
  $$ -y_ix_i * \frac{\exp(-y_i(ω_0 + w^Tx_i))}{1 + \exp(-y_i(ω_0 + w^Tx_i))}$$
  using the sigmoid function,
  $$ -y_ix_i * \frac{\exp(-y_i(ω_0 + w^Tx_i))}{1 + \exp(-y_i(ω_0 + w^Tx_i))} \rightarrow -y_ix_i *\sigma(-y_i(w_0 + w^Tx_i))$$

Then place all derived values back into $\frac{\partial f}{\partial w}$,

$$ \frac{1}{n} \sum_{i=1}^n ((\frac{\partial}{\partial w})\log(1 + \exp(-y_i(ω_0 + w^Tx_i))) + ((\frac{\partial}{\partial w})λ||w||_2^2)) $$

$$\frac{1}{n} \sum_{i=1}^n -y_i *\sigma(-y_i(w_0 + w^Tx_i)) + 2\lambda w $$

$$\frac{\partial f}{\partial w} = - \frac{1}{n} \sum_{i=1}^n y_ix_i *\sigma(-y_i(w_0 + w^Tx_i)) + 2\lambda w $$

Getting $∇_{w’}f$

$$∇_{w’}f = [\frac{\partial f}{\partial w_0}; \frac{\partial f}{\partial w}]$$
$$ = [ - \frac{1}{n} \sum_{i=1}^n y_i *\sigma(-y_i(w_0 + w^Tx_i)) ; - \frac{1}{n} \sum_{i=1}^n y_ix_i *\sigma(-y_i(w_0 + w^Tx_i))+ 2\lambda w] $$

we can combine these terms together to form:

Computing for $ ∇_{w’}^2f$

in order to compute the hessian, we can take a shortcut and find the derivative based on each part of the gradient according to the hessian matrix.

$$ ∇_{w’}^2f = \begin{bmatrix} \frac{\partial^2 f}{\partial w_0^2} \frac{\partial^2 f}{\partial w_0 \partial w} \\ \frac{\partial^2 f}{\partial w \partial w_0} \frac{\partial^2 f}{\partial w^2} \end{bmatrix}$$

we can say that $\frac{\partial^2 f}{\partial w_0 \partial w} = \frac{\partial^2 f}{\partial w \partial w_0}$ due to the rule of derivatives

For the regularization term, the only time we add $2\lambda$ is when the we’re taking $\frac{\partial^2 f}{\partial w^2}$. Therefore, in our matrix, we can just represent the 2nd row and 2nd column ($\frac{\partial^2 f}{\partial w^2}$) for the regularization term. That means we just set the regularization term as $ + \begin{bmatrix} 0 & 0 \\ 0 & 2\lambda \end{bmatrix}$.

Using chain rule for $\sigma(-y_i(w_0 + w^Tx_i))$

• $\nabla_{w_0}$:

  $$ \sigma’(-y_i(w_0 + w^Tx_i)) = \sigma’ * (-y_i(w_0 + w^Tx_i))’\
  = -y_i * \sigma(1 - \sigma)
  $$

• $\nabla_w$:

  $$ \sigma’(-y_i(w_0 + w^Tx_i)) = \sigma’ * (-y_i(w_0 + w^Tx_i))’\
  = x_i * \sigma(1 - \sigma)
  $$

Then we can say for the hessian matrix, we can replace the result of what the partial derivative is for each respective $w$ or $w_0$

$$ ∇_{w’}^2f = \begin{bmatrix} \frac{\partial^2 f}{\partial w_0^2} \frac{\partial^2 f}{\partial w_0 \partial w} \\ \frac{\partial^2 f}{\partial w \partial w_0} \frac{\partial^2 f}{\partial w^2} \end{bmatrix}$$

For $\frac{\partial^2 f}{\partial w_0^2}$:

• $-y_i * \sigma(1 - \sigma)$ since it is $\frac{\partial f}{\partial w_0}$

$$ = - \frac{1}{n} (\sum_{i=1}^n y_i * -y_i * \sigma(1 - \sigma) * \begin{bmatrix} 1\\ x_i \end{bmatrix}) + 2\lambda \begin{bmatrix} 0\\ w \end{bmatrix} $$

$$ = \frac{1}{n} (\sum_{i=1}^n y_i^2 * \sigma(1 - \sigma)) * 1 + 2\lambda \begin{bmatrix} 0\\ w \end{bmatrix} $$

For $\frac{\partial^2 f}{\partial w^2}$:

• $x_i * \sigma(1 - \sigma)$ since it is $\frac{\partial f}{\partial w_0}$

$$ = - \frac{1}{n} (\sum_{i=1}^n y_i * x_i * \sigma(1 - \sigma) * \begin{bmatrix} 1\\ x_i \end{bmatrix}) + 2\lambda \begin{bmatrix} 0\\ w \end{bmatrix}$$

$$ = \frac{1}{n} (\sum_{i=1}^n y_i^2 * \sigma(1 - \sigma)) * x_i + 2\lambda \begin{bmatrix} 0\\ w \end{bmatrix} $$

For $\frac{\partial^2 f}{\partial w \partial w_0} = \frac{\partial^2 f}{\partial w_0 \partial w}$

• $x_i * \sigma(1 - \sigma)$ since it is $\frac{\partial f}{\partial w_0}$

$$ = - \frac{1}{n} (\sum_{i=1}^n y_i * \sigma(1 - \sigma) * \begin{bmatrix} 1\\ x_i \end{bmatrix}) + 2\lambda $$
$$ = - \frac{1}{n} (\sum_{i=1}^n y_i * \sigma(1 - \sigma) * x_i) + 2\lambda \begin{bmatrix} 0\\ w \end{bmatrix} $$
or
$$ = \frac{1}{n} (\sum_{i=1}^n y_i * x_i * \sigma(1 - \sigma)) * 1 + 2\lambda \begin{bmatrix} 0\\ w \end{bmatrix} $$

We can put all of the options from the gradients due to the hessian matrix (representing $x_i$):

$$ \begin{bmatrix} \frac{\partial^2 f}{\partial w_0^2} \frac{\partial^2 f}{\partial w_0 \partial w} \\ \frac{\partial^2 f}{\partial w \partial w_0} \frac{\partial^2 f}{\partial w^2} \end{bmatrix} = \begin{bmatrix} 1 & x_i\\ x_i & x_i^2 \end{bmatrix} $$

Then we can put it together and form:

L2-Regularized Multinomial Logistic Regression

For an extra challenge, here we derive the gradients for the loss function of a l2-regularized multinomial logistic regression

$$f(W, b) = -\frac{1}{n}\sum_{i=1}^n[y_i^T(Wx_i + b) - log(1^Texp(Wx_i + b))] + \lambda||W||_F^2$$

Softmax

(To be updated)

Let us represent the softmax function: $$\text{softmax}(x) = \frac{exp(x)}{1^T exp(x)}$$

Computing for f

Finding $\nabla_W f$:

$$ f(W, b) = $$
$$ -\frac{1}{n}\sum_{i=1}^n[(\nabla_W)y_i^T(Wx_i + b) - (\nabla_W)log(1^Texp(Wx_i + b))] + (\nabla_W) \lambda||W||_F^2$$

• Derive $\nabla_W λ||W||_F^2$:

  $$ = 2\lambda W $$

• Derive $\nabla_W y_i^T(Wx_i + b)$:

  $$ = y_i^Tx_i $$

• Derive $\nabla_W log(1^Texp(Wx_i + b))$:

  using the chain rule twice:
  $$ \log’(1^T exp(Wx_i + b)) * \sum_{l = 1}^K \nabla_W [exp(Wx_i + b)_l] $$

  • apply the log

    $$ \frac{1}{1^T exp(Wx_i + b)} * \sum_{l = 1}^K [exp(Wx_i + b)_l] * \nabla_W [<w_l, x_i>] $$

  • note that $ \nabla_W [<w_l, x_i>]$ is equivalent to $x_i$ since we are taking the cross product of a static $x_i$ given for all ls in the sum, and then the gradient of such would result in $x_i$

    $$ = \frac{1}{1^T exp(Wx_i + b)} * \sum_{l = 1}^K [exp(Wx_i + b)_l] * x_i$$

  • combine

    $$ = \sum_{l = 1}^K\frac{[exp(Wx_i + b)_l]}{1^T exp(Wx_i + b)} * x_i$$

  • use softmax

    $$ = \sum_{l = 1}^K softmax(Wx_i + b)_l * x_i$$

$$ = softmax(Wx_i + b) * x_i$$

plug in for the main equation

$$ \nabla_W f(W, b) = -\frac{1}{n}\sum_{i=1}^n[y_i^Tx_i - softmax(Wx_i + b) * x_i] + 2\lambda W$$
$$= -\frac{1}{n}\sum_{i=1}^n(y_i^T - softmax(Wx_i + b)) * x_i + 2\lambda W $$

Finding $\nabla_b f$:

• Derive $\nabla_b λ||W||_F^2$:

  $$ = 0$$

• Derive $\nabla_b y_i^T(Wx_i + b)$:

  $$ = y_i$$

• Derive $\nabla_b log(1^Texp(Wx_i + b))$:

  using the chain rule twice:
  $$ = \log’(1^T exp(Wx_i + b)) * \sum_{l = 1}^K \nabla_W [exp(Wx_i + b)_l] $$

  • apply the derivative again due to the exponent

    $$ \frac{1}{1^T exp(Wx_i + b)} * \sum_{l = 1}^K * [exp(Wx_i + b)_l] * \nabla_W [<w_l, x_i>] $$
    since we are finding the gradient in respect to b, we can cancel out terms:
    $$ \frac{1}{1^T exp(Wx_i + b)} * [exp(Wx_i + b)_l] $$

  • add the summation back

    $$ \sum_{l = 1}^K \frac{exp(Wx_i + b)_l}{1^T exp(Wx_i + b)} $$

  • use softmax

    $$ \sum_{l = 1}^K softmax(Wx_i + b)_l $$
    $$ softmax(Wx_i + b) $$

Put it all together

$$ \nabla_b f(W, b) = -\frac{1}{n}\sum_{i=1}^n y_i - softmax(Wx_i + b) $$

Both results

Empirically verify our derivation utilizing PyTorch

Here we will use PyTorch as a tool to evaluate the gradient, then we will apply our own solution to get a result.

Load and prepare a dataset

Using sklearn wine dataset and one hot encode the targets

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

from sklearn.datasets import load_wine
from sklearn.preprocessing import OneHotEncoder

wine_data = load_wine()
X_wine = wine_data.data
Y_wine = wine_data.target

# add to Y dim
Y_wine = Y_wine.reshape(-1, 1)

enc = OneHotEncoder(sparse_output=False)
enc.fit(Y_wine)
Y_onehot = enc.transform(Y_wine)

n, d = X_wine.shape
n, k = Y_onehot.shape

# convert to pytorch
Y_onehot = torch.from_numpy(Y_onehot).to(torch.float)
X_wine = torch.from_numpy(X_wine).to(torch.float)

# init parameter tensor (w) with bias (w0 = 1)
def init_weights_wine(d, k):
  w = torch.ones((d, k), device=device, requires_grad=True)
  w = w/(len(X_wine)) # prevent overflow from exp
  w.retain_grad()
  return w

def init_bias_wine(k):
  b = torch.ones((1, k), device=device, requires_grad=True)
  b = b/(len(X_wine)) # prevent overflow from exp
  b.retain_grad()
  return b

W_test = init_weights_wine(d, k)
b_test = init_bias_wine(k)

Define the loss function for MLR

Define the function so that we can call .backward() from pytorch and evaluate it from our answer.

Loss function

1
2
3

# the loss function for l2 regularized multinomial logistic regression
def f_multi(X, Y, W, b, lambda_v=0):
    return -torch.mean(torch.sum((Y * torch.matmul(X, W) + b), dim=1) - torch.logsumexp(torch.matmul(X, W) + b, dim=1)) + lambda_v * torch.norm(W, 'fro')**2

Prepare and compare both our solution and pytorch

Evaluate the gradient using pytorch

1
2
3
4
5
6
7
8

W_pytorch = init_weights_wine(d, k)
b_pytorch = init_bias_wine(k)

W_pytorch.grad = None
b_pytorch.grad = None

loss = f_multi(X_wine, Y_onehot, W_pytorch, b_pytorch, lambda_v=1)
loss.backward()

Define and evaluate our derivation

1
2
3
4
5
6
7
8
9
10

# the loss function for l2 regularized multinomial logistic regression
def f_multi_grad_w(X, Y, W, b, lambda_v = 0):
  logits = torch.matmul(X, W) + b
  return -torch.matmul((Y - torch.softmax(logits, dim=1)).T, X) / len(X) + 2 * lambda_v * W

my_W = init_weights_wine(d, k)
my_b = init_bias_wine(k)

myWGrad = f_multi_grad_w(X_wine, Y_onehot, my_W, my_b, lambda_v=1)
myBGrad = f_multi_grad_b(X_wine, Y_onehot, my_W, my_b)

Empirical Results

Weight gradients

1

torch.norm(W_pytorch.grad, 'fro') - torch.norm(myWGrad, 'fro')

tensor(4.5776e-05, grad_fn=)

Bias gradients

1

torch.norm(W_pytorch.grad, 'fro') - torch.norm(myWGrad, 'fro')

tensor(-2.9802e-08, grad_fn=)

License

This work is licensed under CC BY-NC-SA 4.0

Share